
All of these are valuable, even if the other 30,999,999,999,961 digits aren’t.\( \newcommand\) Find the dimensions of the box that minimizes the amount of material used. Our objective is to find the optimal non-overlapping packing of a collection of general (non-identical) ellipses, with respect to a container circle that has. We need to deal with questions about the accuracy of floating point arithmetic, questions of estimations and error bounds, and questions concerning optimization. The two configurations are shown below with their. Hence the width W of the rectangle is give by. Using Geometry Expressions, we determine the angle of the fan in terms of aspect ratio (a) and radius. I haven't found any good page on evaluating if a number of given circles is able to fill a rectangle. with a minimum radius of N homogeneous circles covering a square. Many covering problems are concerned e.g. It's difficult to find some good information on this. Let (x,y) be the coordinates of the top left vertex of the rectangle. I understand, your problem then becomes a covering problem, not a packing problem.
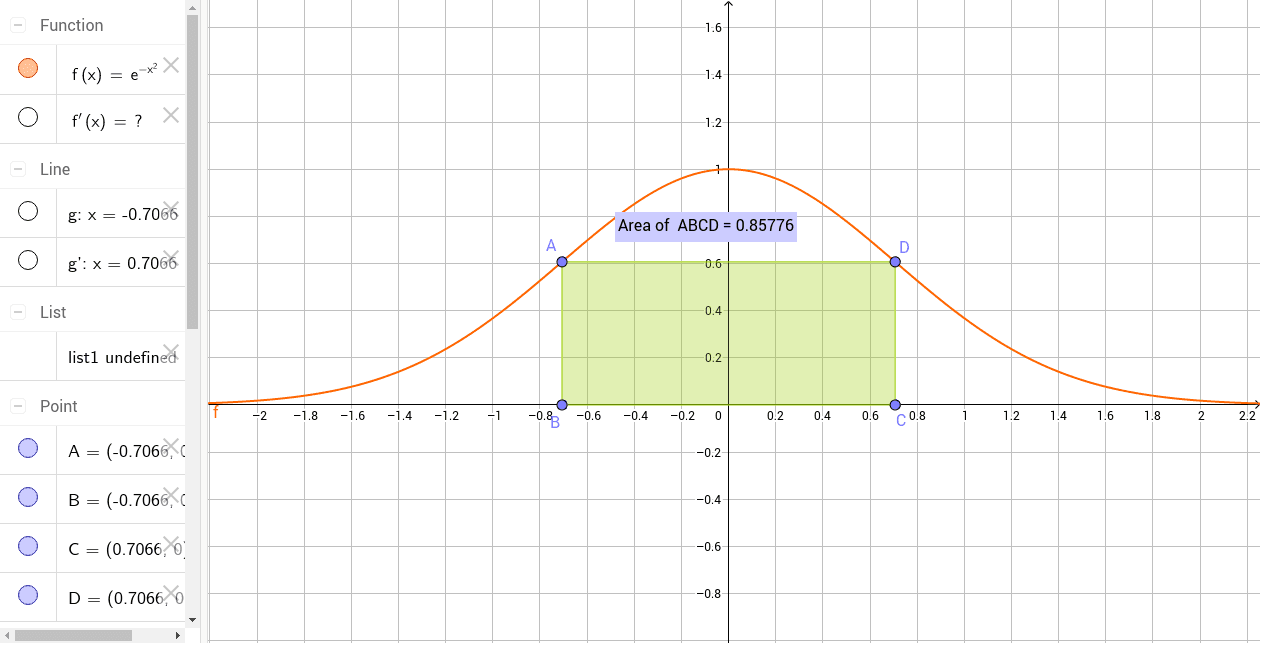

The slope m1 of the line through OB is given by. Find the largest possible volume of such a cone.1. We first need to find a formula for the area of the rectangle in terms of x only. But that doesn’t mean this isn’t valuable! To generate these approximations, we use many important tools from Mathematics, Computer Science, and Computer Engineering. A right circular cylinder is inscribed in a cone with height h and base radius r. But why do we care? If you give me the first 39 digits of pi, I can tell you the width of the known universe within one hydrogen atom (See Numberphile’s video for how). There are many ways to calculate the digits of pi - you can use random sampling, geometry, calculus, etc. But I started wondering how do we know that? How do we make pi? Journal of Global Optimization 43 (2009), 299-328 Keywords: nonlinear programming, global optimization, cutting stock problem, circle packing problem, shape. And since the 6th grade, I’ve known Pi is 3.14 and some change. outdoor track is to be created in the shape of a rectangle with semicircles attached on. The diagonal of the rectangle will be the diameter of the circle. An other interesting consequence of this is that the two shaded shapes here (the quarter circle and the circle with half the radius) have the same area. On Pi Day of this year, Emma Haruka Iwao calculated pi to 31 trillion digits, dwarfing the previous record of 22 trillion digits. Let ABCD be the rectangle inscribed in the circle with center O and radius (r).


 0 kommentar(er)
0 kommentar(er)
